TLDR; A tube’s stiffness goes up with the 4th power of radius, but weight only goes up with the square. For a LowRider build, the 1.25" x 0.49" DOM steel tube from speedymetals.com should improve stiffness and reduce weight.
I’ve been reading the forums the past few days and thought I would chime in. My background is as a Mechanical Engineer and I hope there are some things I learned and applied in my careers which could be useful to this incredible community.
To paraphrase another poster, there’s “math” and then there’s MATH. This post spends more time on the latter, and should give a brief primer on the underpinnings of simple design choices.
Terms of the art (in particular stiffness)
Discussing this topic is hard because the terms have a scientific meaning and a colloquial meaning. There’s enough overlap that we confusingly talk about one when we mean the other. For instance, stiffness is an extrinsic[1] property of an object. If you slice a board in half it loses stiffness. Elasticity, on the the other hand is an intrinsic[1] material property. If you cut a spring in half it is just as springy. However, you will frequently hear stiffness to refer to a metal, and that’s just language being messy. So in order to clear up confusion, when I mean a material’s intrinsic quality, I’ll refer to it as stiffness (MOE) even though we know I really mean Modulus of Elasticity[2].
There’s also the term bending moment of inertia, which is easily confused with other similar equations, specifically rotational moment of inertia[3] and section modulus[4]. Since these basically differ only in the exponential, it’s easy to confuse them and yet get radically different results. Any time I refer to inertia I mean “bending moment of inertia”.
So what makes something stiff?
It’s a combination of shape and material. If the material is stiff (MOE) and the shape has high bending moment of inertia, then the result will be hard to bend (i.e. stiff). If you take the same material and make a low (bending moment of) inertia object, then it will be less stiff. This is why rods are much less stiff than tubes.
Stiffness is linear with inertia. If you double inertia, you double stiffness. However, inertia increases with the fourth power of dimension. So if you double a rod’s radius, you increase the inertia (and thus the stiffness) by 2^4 = 16 times!
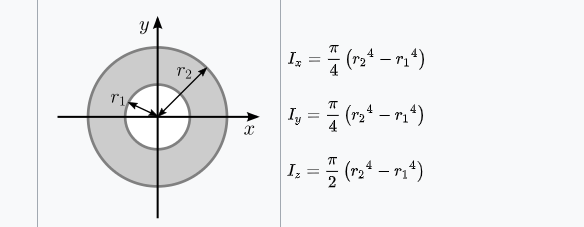
The cool thing is that at the same time you only increased weight by 2^2 = 4 times (because weight increases with area). So going up in radius is hugely beneficial relative to weight.
Another neat thing about calculating both weight and inertia is that they are “superpositionable” calculations. In other words, weights can be added to weights and inertias to inertias. Where this comes in handy is that you can add “negative weight” and “negative inertia”. In other words, you can calculate the weight and inertia of a tube by adding the weight/inertia of the positive outside diameter and then SUBTRACT the weight/inertia of the missing inside diameter.
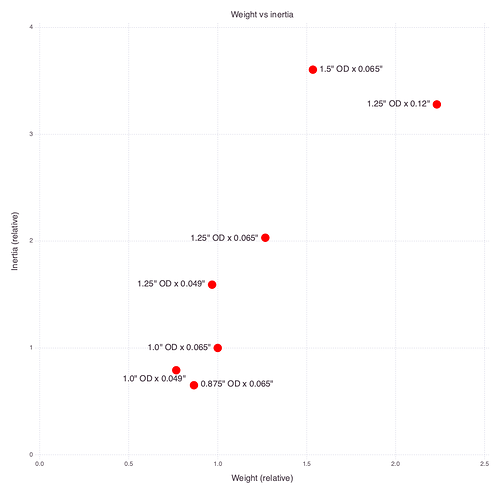
Here’s a simple graph showing relative inertia for tubes of various ODs and wall thicknesses which are available from speedymetals.com (DOM steel). I’ve referenced everything to LowRider’s default 1" OD x 0.065" wall thickness, so if it’s to the left it’s lighter and if it’s above it’s stiffer.
We can see that 1.25 x 0.049" is a potential winner! It’s lighter (faster machine movements) and stiffer (less deflection). The downside is that the wall is thinner, and this could lead to flattening of the tube if the forces are too high.
And if you wanted to go significantly stiffer for not much increase in weight, the 1.5 x 0.065" is a strong candidate.
Now, this is MATH. The real world is going to closely track this, so long as everything else is as perfect as the MATH. (Hah!)
In the real world, you’ll get various grades of metal, alloys, and treatments. All those factors impact stiffness (MOE) and can easily sway the resulting numbers by ± 20%. Which is how EMT can have a higher inertia but an overall lower stiffness.
Why do real-world tests show such variation?
This can be completely chalked up to materials, tolerances, and fabrication. It’s why it’s so important to find quality suppliers, and why it’s hard to compare across suppliers, stores, and shores. And to test, test, test. Because MATH hints at, but does not equal, REALITY.
Follow up thoughts:
Should we talk about strength?
Nope.
It’s only relevant if the parts are breaking. As @vicious1 has written in other places, he’s seen calculated loads on the order of 1-2kg. Until the loads get 100x higher we can safely ignore strength as an issue.
Fun fact: all metals have about the same stiffness (MOE)
It’s just one of those peculiar qualities of metals. Like almost all are silver-ish (Copper and Gold being the exceptions).
So most metals naturally have similar (within an order of magnitude) stiffness (MOE). That means that careful choice of metals is essential because quality, alloy, and treatment make a big difference.
But what about titanium? It’s pretty magical stuff, right?
TLDR; Titanium alloys are only better for us when the tube dimensions are larger than the equivalent for steel.
Titanium is awesome, but it’s not a magic bullet. Titanium is very tough. It has an incredibly high rupture resistance vs steel (1080MPa vs 300MPa), which tells us that it really doesn’t like to break. And it’s much harder than steel (3700 Mpa vs 2100), so it wears much better.
However, it is not as stiff (MOE) as steel (200GPa vs 120Gpa) and it is not as light as aluminum (2.7g/cm^3 vs 4.5 g/cm^3). So for identical dimensions to steel (or identical mass to aluminum) it’s going to perform worse in a stiffness application. If you can get larger-diameter thinner-walled titanium tubing than it winds up being stiffer AND stronger AND lighter AND higher wearing. But only because you got it BIGGER.
What about carbon fiber?
It’s great stuff in the right application! Stiff(MOE) as all get out and light as a feather, but it has very poor wear characteristics and does not fail gracefully. It’s the same game as titanium; you can get lighter, stronger, stiffer so long as you go BIGGER.
What about XXX?
I’m happy to discuss XXX in this thread. I’ve seen ideas such as:
- pretensioning
- unfortunately only works when you want to avoid a material changing from compression to tension. Sailboat and bridge rigging qualifies, but the case of a CNC gantry does not
- filling in the tube
- decreasing returns by a power of 4, so you quickly add weight without rigidity
- using other cross-sections
- much higher inertia, but at what cost? It’s been described elsewhere in the forums how important the round tube’s symmetric profile is for ease of alignment and calibration.
Throw some ideas out there, there are no bad questions and the worst that will happen is we’ll all learn together.
Footnotes
[1] Extrinsic properties are, roughly speaking, properties which change if you cut something into parts. For instance, a board’s length is extrinsic because if you cut it in half, it’s length changes.
On the flip side, intrinsic properties are things which stay constant even if you change the quantity of material. A board’s density does not change if you cut it in half, a glass of water’s temperature does not change if you pour half of it out.
[2] Modulus of Elasticity, aka Young’s Modulus, is a scientific term which, roughly speaking, tells us how far something will deflect for a given force. If the MOE is twice as high, the material will deflect half as much. If it is twice as low, it will bend twice as much. MOE goes from really high for graphene (1,000GPa) to really low for rubber (0.01GPa). So a rod made out of graphene would literally deflect 100,000 times less than the same rod out of rubber.
[3] Rotational moment of inertia is roughly speaking how much energy is in a spinning object. We all know that a bike wheel is light but has a lot of spinning energy whereas a solid wooden block is a lot easier to stop spinning.
[4] Section modulus is used to determine at what load an object will break.



 sorry it hasn’t been released yet:sunglasses: stay tuned
sorry it hasn’t been released yet:sunglasses: stay tuned