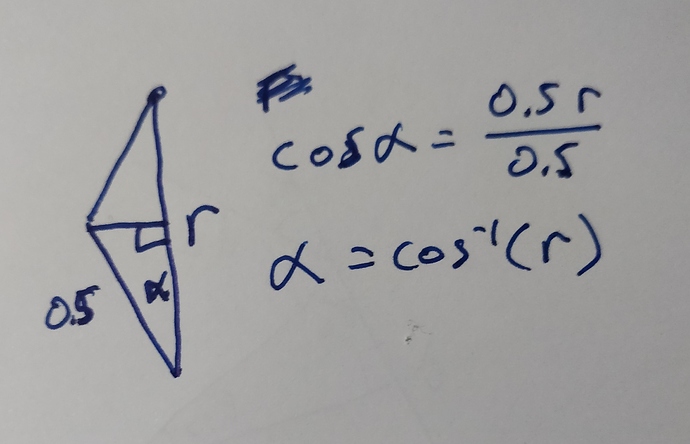I will update you later today or tomorrow. Thanks!
The way this 2 axis scara works is that arm1 and arm 2 are both 100mm long. Arm1 ( the green one) rotates about the center and arm2 ( the red one) rotates about the end of arm1 independently. For example, if I rotate arm2 to 45 degrees relative to the machine x axis, then I rotate arm1 to any angle, arm2 angle stays at 45 degrees relative to the machine x axis. It’s a cool design that both arms rotate individually and the rotation angle of the second axis is not dependant on the rotation angle of the first. But of course the location of the endpoint of arm2 changes as arm1 rotates.
In my attempt to create patterns I wrote a VB program ( could use any language,) that reads xy values by stripping the values out of a sandify ( or other) gcode file, converts them to arm1 angle and arm2 angle and writes out a new gcode file to run on the machine. This new gcode file rotates to the proper arm angles. Example: G01x150y35 calculates that arm1 angle should go to 26.4989 degrees and that arm2 angle should go to 52.767 degrees.
This verifies correctly in my cad system, as long as I am working in the first quadrant.
Now, sending a value of G01 X6.0 will rotate arm1 360 degrees. ( Same with arm2 with G01 Y6.0 will rotate arm2 360 degrees.) Based upon this 1 degree of rotation for either axis is .016666. So, if I send the command G01X-0.441647704579837 Y 0.879446696923409 I get to the arm1 26.49 degrees and arm2 52.767 degrees placing the magnet at the correct x150 y35 location.
To sum up open issues…
- My working circle is 400mm dia. Not sure if I should consider x0y0 ( center of circle) to be program zero or x200 y0 to be program zero, or if it will matter as I get deeper into this.
2)I’m not sure if I should change my stepper motor values so that one rotation is some other value than 6.0. I don’t think it matters as long as I know what the value is and use it correctly in my calculations.
I have both arms turning cclw with a positive value. I think this is also just a convention to be aware of while programming and not important.
-
Every position will have two solutions for arm1 and arm2 angle. I don’t know when or if I am going to care to control that.
-
all motions between 2 points are going to be arcs due to the mechanics of the machine, so to generate (draw) a semi straight line, large moves will have to be broken down into smaller line segments. This should be fairly easy programmatically but I think it is ( perhaps?) going to be joined with the issue of choosing which of the 2 solutions of arm angles to use. It may be a secondary consideration though.
-
I think the issue of solving getting correct arm angles for values in all 4 quadrants is the number one priority and after that work out the other issues.
Final thoughts… Possibly this wheel has been invented before? So I have done a bit of searching on inverse kinematics and someone said that using “fuzzy logic?” is a good method. Someone else said that building a huge array lookup table is a good method. Another thing I was looking up is Matlab but that looks pricey and this is a random hobby for me so spending out for software is probably something I’m not going to consider to make fancier sand patterns and working through this sort of thing is half the fun of it anyway! Please let me know if you need more clarification or information of any kind. I can clean up and send you the VB program I have so far if that helps. I think I will post it just in case you can make anything of my thought process from it.
'Here is the Visual Basic program I have written so far;
’ It probably has some junk in it for testing purposes.
Imports System.Math
Module Module1
Sub Main()
FileOpen(1, "g:\t1.gcode", OpenMode.Input)
FileOpen(2, "g:\t1.ngc", OpenMode.Output)
Print(2, ("$HX"))
Print(2, vbCrLf)
Print(2, ("$HY"))
Print(2, vbCrLf)
Print(2, ("G01X0.00 Y0.00 F50"))
Print(2, vbCrLf)
Dim xval As Decimal
Dim yval As Decimal
Dim angle1 As Decimal
Dim angle2 As Decimal
Dim armlength As Decimal = 100
Dim arm1_angle As Decimal
Dim arm2_angle As Decimal
Dim a4 As Decimal
Dim angle4 As Decimal
Dim half_dist As Decimal
Dim dist As Decimal
Dim yxval As Single
Dim xtxt As String
Dim ytxt As String
' Dim tval As String
' Dim Endx As Integer
Dim line As String
Dim test As Decimal
Dim test2 As Decimal
Dim nval As Integer = 1
While Not EOF(1)
line = LineInput(1) 'start getting data lines
Dim SearchWithinThis As String = (line)
Dim SearchForx As String = "X"
Dim FirstxCharacter As Integer = SearchWithinThis.IndexOf(SearchForx)
' Dim Nvalx As Integer = (FirstxCharacter)
Dim SearchForY As String = "Y"
Dim FirstyCharacter As Integer = SearchWithinThis.IndexOf(SearchForY)
Dim side1 As Decimal 'right is 0 left is 1 used to mark quadrant 1 and 4 or 2 and 3
Dim updown As Decimal 'top is 0 bottom is 1 used to mark quadrant 1 and 2 or 3 and 4
Dim quadrant As Decimal
xtxt = Mid(SearchWithinThis, 5, 11)
Dim Xtxtdec As Decimal = Val(xtxt)
If Xtxtdec >= 0 Then
side1 = 0 'quadrant 1 or 4
Else
side1 = 1 'quadrant 2 or 3
End If
' Print(2, "The y ppoint value is ")
ytxt = Mid(SearchWithinThis, (FirstyCharacter + 2), (FirstyCharacter + 6))
Dim Ytxtdec As Decimal = Val(ytxt)
If Ytxtdec >= 0 Then
updown = 1 'quadrant 1 or 2
Else
updown = 0 'quadrant 3 or 4
End If
If side1 = 0 And updown = 1 Then
quadrant = 1
ElseIf side1 = 1 And updown = 1 Then
quadrant = 2
ElseIf side1 = 0 And updown = 0 Then
quadrant = 4
ElseIf side1 = 1 And updown = 0 Then
quadrant = 3
End If
Print(2, "the quadrant is ")
Print(2, quadrant)
Print(2, vbCrLf)
'------------------------------------------------------
'------
'calculate dist using sqaroot of (xval squared) + ( yval squared)
dist = Math.Sqrt((Xtxtdec * Xtxtdec) + (Ytxtdec * Ytxtdec))
half_dist = (dist * 0.5)
Dim dd As Decimal
Dim de As Decimal
Dim a1 As Decimal
Dim a2 As Decimal
' Dim xval As Decimal = Xtxtdec
' Dim yval As Decimal = Ytxtdec
If Ytxtdec = 0 Then
Ytxtdec = 0.001
End If
dd = (Math.Atan(Xtxtdec / Ytxtdec))
a1 = (dd * 180 / PI)
'Print(2, "the first angle A1 is")
'Print(2, a1)
'Print(2, vbCrLf)
'
'------------------------------------------
dd = (Math.Acos(half_dist / armlength))
a2 = (dd * 180 / PI)
'--------------------------------------------------------
'calculate arm 1 angle (from x axis) subtracting angle1 and angle2 from 90 degrees
Print(2, "Arm 1 angle from x axis is ")
If quadrant = 1 Then
arm1_angle = (90 - (a1 + a2))
ElseIf quadrant = 2 Then
arm1_angle = (180 - (a1 + a2))
ElseIf quadrant = 3 Then
arm1_angle = (270 - (a1 + a2))
ElseIf quadrant = 2 Then
arm1_angle = (360 - (a1 + a2))
End If
Print(2, arm1_angle)
Print(2, vbCrLf)
'------------------------------------------------------
'-- 'calculate angle 4 value
a4 = (180 - (2 * a2))
'Print(2, "Angle 4 is ")
'Print(2, a4)
'Print(2, vbCrLf)
'-------------------------------------------
'arm2_angle Is 180 minus angle4
arm2_angle = arm1_angle + (180 - (a4))
'try adding this in
Print(2, "Arm 2 angle is ")
Print(2, arm2_angle)
Print(2, vbCrLf)
' Print(2, vbCrLf)
'---------------------------------------------
'Convert arm1 and arm2_angle values to gcode values
'one rev of x or y is 6mm" ex:G01X6 moves one revolution
'1 degree move = .0166666mm
Dim ang_to_mm As Decimal
Print(2, "G01X")
xval = arm1_angle * 0.0166666
Print(2, xval)
Print(2, "Y")
yval = arm2_angle * 0.0166666
Print(2, yval)
Print(2, vbCrLf)
'nval = nval + 1
End While
FileClose(1)
FileClose(2)
End Sub
End Module
Ok. This is enough for me to get started. Give me a few days to take a look. It seems like we can get there, for sure.
You don’t need fuzzy logic for this, it is directly solvable.
A lookup table won’t work either, because it will not compensate for when you rotate more than one full rotation.
Matlab is great, but it is really just a programming language and a bunch of tools. You can really do just as much with python and matplotlib. Definitely don’t buy it to solve one math problem.
The steps/unit is somewhat important because Marlin only reads a few characters past the decimal. So you don’t want X0.0001 to be too much different than X0.0002. There are also acceleration and max speeds to consider.
I’m excited to work this out. I have a solution I think will work, but I’d like to try it a bit first.
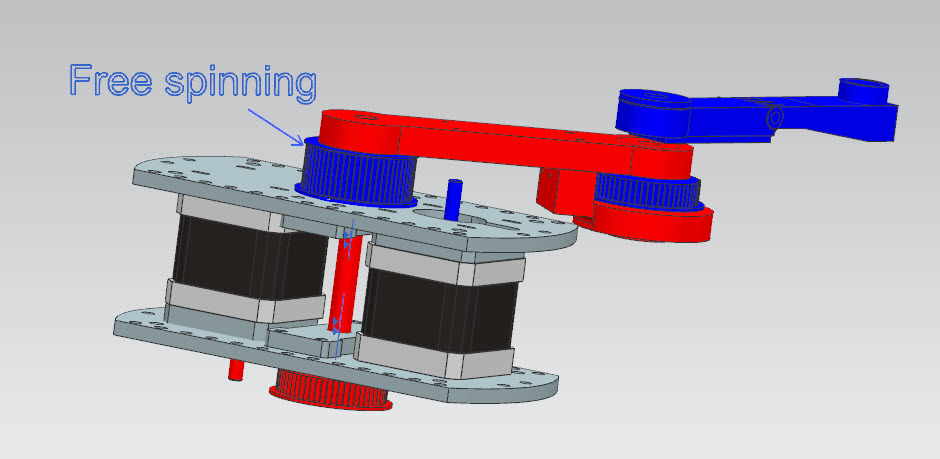
I hope this cad picture helps in understanding the scara arm. The red objects rotate arm1 and the blue rotate arm2. All of the driving pulleys are the same diameter ( same number of teeth as well.) I’m including a few actual pictures as well.
I couldn’t wait. This is just too interesting.
First, I am going to again push for using the theta rho output. Just because it has a lot of the same challenges and I’ve solved them in sandfy. 1) I use a ton of vertices to create lines, so you won’t have to. 2) I am keeping track of movements around the circle, and I am outputting the angle in a continuous angle. So when a line goes from quadrant 4 to 1, the angle is greater than 2pi. 3) It makes the math much simpler.
I’m going to explain the math. Then I will make a quick program to do the conversion (It will be a fun challenge). Then, we can talk about what other challenges remain.
Math
Sorry for the chicken scratches, I am writing this out on paper.
Theta Rho
Theta, Rho is the sisyphus format. It is an angle and a radius.
The radius is always between zero and one. So even though you have 200mm radius, the max rho is 1.0.
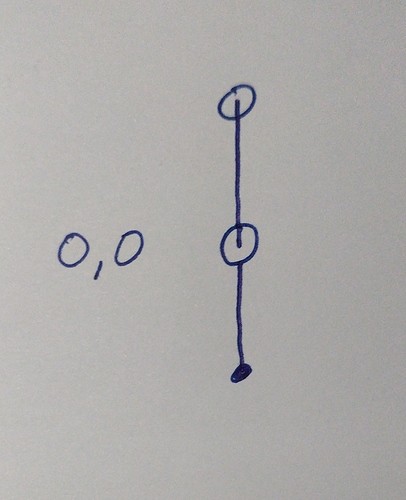
Theta is the angle, and it always is continuous. It is in radians, and can be positive or negative. This is a simple pattern that would clear the table with 100 turns:
0,0
200*pi, 1.0
0,0
Let’s make zero on your motors straight ahead. Let’s also make this 0,1 in theta rho. Each of your arms are 0.5r long.
Rho
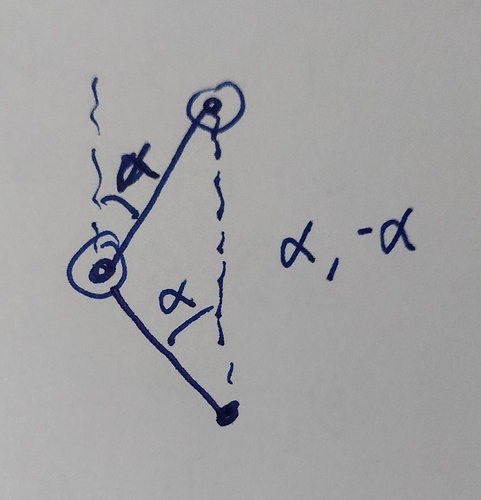
Let’s always assume your arm can only bend one way. It is really neat that it goes both ways, but it isn’t important which way, and we might as well make it easy on ourselves.
If we want to keep theta at 0, but make r something else, we can do this:
When we do that, the first motor is at alpha and the second is at -alpha. We’ll calculate alpha in a minute.
Theta
So, if we add an angle to both motors, we will move theta, but not Rho.
So we have:
Motor1 = theta + alpha
Motor2 = theta - alpha
Alpha
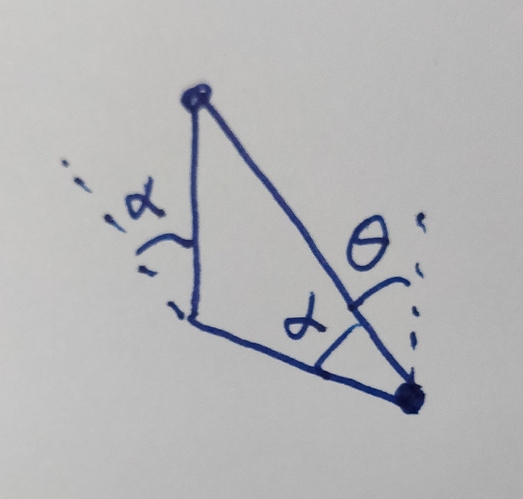
Going back to the triangle when we first saw alpha, we can split it into two right triangles. In the closer triangle, the hypotenuse is 100mm, but we know that is 0.5 in our normalized size. The height is half of Rho, so we have:
cos(alpha) = 0.5 * r / 0.5 = r
alpha = cos^-1(r)
Motor Output
Motor one (in the middle) I’ll call M1. Motor two (on the arm) is M2:
M1 = theta + cos^-1(rho)
M2 = theta - cos^-1(rho)
Those are in radians. So to get gcode X, Y, we need to multiply by 6.0/(2pi).
Code
Sorry, I don’t know visual basic well, and I run linux, so I don’t think there’s a good way for me to run it. I took a stab at implementing this in python though. I went ahead and used an online editor, so you can go there and try it, without needing python on your machine.
import math
# Config
MOTOR_1_UNITS_PER_ROTATION = 6.0
MOTOR_2_UNITS_PER_ROTATION = 6.0
INPUT_NAME = 'sandify.thr'
OUTPUT_NAME = 'transformed.gcode'
# Open the files.
with open(INPUT_NAME, 'r') as infile:
with open(OUTPUT_NAME, 'w') as outfile:
for line in infile:
# First, separate by content and comments
parts = line.strip().split('#')
if len(parts[0].strip()) == 0:
# This line doesn't have anything that isn't a comment
outfile.write(line.replace('#',';'))
continue
else:
(theta, rho) = parts[0].split()
# Here, we're actually doing the math.
m1 = float(theta) + math.acos(float(rho))
m2 = float(theta) - math.acos(float(rho))
x = MOTOR_1_UNITS_PER_ROTATION * m1 / (2*math.pi)
y = MOTOR_2_UNITS_PER_ROTATION * m2 / (2*math.pi)
outfile.write("G1 X{:0.03f} Y{:0.03f}\n".format(x, y))
# We just moved each motor a bunch. A whole lot.
# When we start the next file, we don't want it to unroll
# So we will make the current coordinate something that is small, but the same.
xmod = x % MOTOR_1_UNITS_PER_ROTATION
ymod = y % MOTOR_2_UNITS_PER_ROTATION
outfile.write("G92 X{:0.03f} Y{:0.03f} ; Reset the coordinates\n".format(xmod, ymod))
In that repl website, you can upload a sandify.thr file, and hit run. It will write out the transformed.gcode file, which you can inspect and down.
Running it.
Do you have endstops? You’ll want to make sure the machine starts upright with both arms fully extended, and set to X0 Y0.
At the end, it will have X,Y values out in the hundreds or thousands. When you start the next one, you don’t want to have to reset it, and you don’t want to have to unwind the whole thing. So I added a G92 at the end of the file. You will want to make sure you do things like select the always end on perimeter function in sandfy and then maybe add a G1 X0 Y0 to the end of the file to bring it around to the top again.
If you have resolution problems, you can reduce the steps/mm in Marlin, and increase the config constants in the script. at 6000 segments/revolution, we have a resolution right now of 0.06degrees. That seems about right to me.
This is the pattern I made to test it out:
transformed.gcode (34.8 KB)
More Thoughts
This was really interesting and I couldn’t stop thinking about it. Thank you for sharing it. I hope all of this is clear, and I obviously didn’t try it on a machine, so I hope got it close to right. I was shooting for clarity, but I can sometimes lean into condescending. This is a tricky problem, I know. I hope I didn’t completely miss the mark.
Wow, you have given me a lot to review here. Thanks much! I don’t have end stops per se, rather I am using two hall effect transistors and magnets to home each axis. On a machine like this I want to be able to locate a repeatable zero location but not have any stops since it can rotate to infinity. I am using bCNC and it very nicely allows me to move the arms from home position to anywhere and call it machine zero and it remembers that location for the next session as 0,0. I will try playing with this and let you know what I can or cannot make sense of.
Wow, the transformed.gcode file worked! VERY cool! At the end the trail went off to the left instead of the right but that is just a setting in the code or in grbl. Since it’s Fathers Day and we are hosting a party today I probably wont have time to look at much more today but this is a great start! Thanks Jeff.
John
 Great!
Great!
Happy Fathers Day! I am enjoying some family time this morning myself.
Ok, so wow, I just figured out that I can run Python in Visual Studio so I ran your program after pulling down a polar.thr sysiphus file and executing your program. I ran it on my table and it’s perfect! What I thought was probably going to be weeks of work banging my head against a wall, you solved in less than a day! Thanks! You rock!
Awesome. If you don’t mind, please share a video of it cruising with some sandify design. It is a cool machine, you did the hard work, for sure.
Heffe, there’s a .NET implementation for Linux, https://www.mono-project.com/docs/about-mono/languages/visualbasic/ that should compile and run VB on your system.
Oh. I thought mono was for C#. I will check it out. Thanks.
That’s interesting. So the good news is you can run VB on linux. The bad news is you can run VB on linux.
I’m curious, since Marlin is only thinking of the speeds and accelerations of those two angles, how bad the problem of speed variance is going to be. It will be a lot faster on the edge than the middle of the table. I think we could try to force the kinematics into Marlin, and it would be able to keep the ball going at a constant speed, but then the problem becomes the actual motors may need to be going at blazing speeds when the ball is near the middle.
That seems like a lot of work. Mostly because I assume the motion system in Marlin is written to be efficient and not particularly flexible or clear.
But maybe, since we have a ton of vertices in the script, and we know the coordinate frames of the motors and the thr, we can create better speed limits based on the ball speed, and convert them to motor speeds, and then let Marlin manage the max speed and accelerations to keep the motors and arms comfortable.
I would think you could add the feedrate as part of the transformation. Assuming the path is broken into sufficiently small segments (which would be needed anyway for the paths to match the IK model) the desired cartesian speed could be mapped into time elapsed for the segment, which could then be converted into motor feedrates after the incremental rotations are known. And those feedrates could be capped during the transformation or in the firmware. Either way, the speeds should obey the cartesian speeds as long as the motors can keep up, otherwise it’s clamped and it may move slower than requested.
Here is a youtube video of the machine running.
That is really cool. I like the little unreachable corners filled with items you’d find on the beach. Thanks for sharing.
Beautiful stuff! I agree with Jeff, the seashells are an artistic touch 

Goodness @jeffeb3, this is awesome!
I don’t think I have ever witnessed this much helpfulness in any forum in any field ever